Линейное уравнение первой степени с двумя переменными.
Линейное уравнение первой степени с двумя переменными – это уравнение вида ax + by = c, где x и y – неизвестные, a, b, c – некоторые числа, при этом хотя бы одно из чисел a и b не равно нулю. Числа a и b называются коэффициентами при неизвестных, c – свободным членом.
Подобное определение не всегда сразу понятно, и, безусловно, требует дополнительных разъяснений. Попробуем объяснить.
Что означает уравнение с двумя переменными?
Тут все просто. Это уравнение, в котором присутствует сразу два неизвестных числа. Для какой задачи мы можем использовать подобную математическую модель? Например, в 7 Б классе учатся 18 человек. Причем неизвестно, сколько девочек и сколько мальчиков. Пусть мальчиков будет x, а девочек y. Таким образом, у нас получается такое уравнение:
x + y = 18. Заметим, что у нас много вариантов значений x и y, при которых наше уравнение обратится в верное числовое равенство. Например, x = 10, y = 8 или x = 5, y = 13 и т.д.
Такую пару чисел, при которой уравнение с двумя переменными обращается в верное равенство, называют решением уравнения. К примеру, x = 2 и y = 16 – решение уравнения x + y = 18. Это решение можно записать и в кратком виде - (2; 16). Важно при этом соблюдать порядок записи чисел. В уравнении вида ax + by = c решение записывается именно в таком порядке – (x; y). То есть сначала x, потом y.
Насколько много решений у уравнения с двумя переменными?
Обычно, если коэффициенты a и b не равны нулю, решений уравнения с двумя переменными бесконечное множество. Действительно, если подставлять в уравнение значения x, всегда можно будет определить соответствующее значение y, при котором уравнение обратится в верное равенство. Но бывает и такое, когда уравнение с двумя переменными не имеет решений. Такое возможно, когда, например, коэффициенты a и b равны нулю, а свободный член c ≠ 0.
Что означает уравнение первой степени?
Это означает что степень, в которую возводятся переменные этого уравнения – 1. То есть, у нас нет в уравнении переменных, которые мы возводим в квадрат, куб, четвертую степень, извлекаем корень и т.д.
Что означает линейное уравнение?
Линейное уравнение – это уравнение прямой линии. В этом легко убедиться, вспомнив понятие координатной плоскости. Мы знаем, что каждой паре чисел соответствует единственная точка на координатной плоскости. Теперь возьмем, к примеру, уравнение x + y = 2. Во множество решений данного уравнения попадают такие пары чисел: (0; 2), (2; 0), (1; 1), (5; -3), (-2; 4). Построим эти точки и проведем через них прямую m.
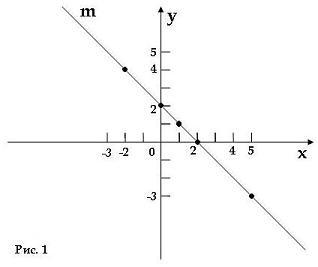
Мы получили график прямой m. Каждая точка этой прямой имеет координаты, являющиеся решением уравнения x + y = 2, или еще говорят, что каждая точка удовлетворяет уравнению x + y = 2. Вообще для того чтобы построить прямую, достаточно найти 2 пары чисел, удовлетворяющих линейному уравнению. И через точки с данными координатами можно строить прямую.
Дата публикации:
Теги: алгебра :: 7 класс :: линейное уравнение
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
- Уроки математики, методические рекомендации к учебнику для 1 класса, Пособие для учителей, Истомина Н.Б., Немкина Е.С., Попова С.В., Редько З.Б., 2013
- Методика обучения математике в начальной школе, Зайцева С.А., Румянцева И.Б., Целищева И.И., 2008
- Алгебра и начала математического анализа, книга для учителя, 11 класс, базовый и профил, уровни, Потапов М.К., Шевкин А.В., 2009
- Алгебра и начала математического анализа, книга для учителя, 10 класс, Потапов, Шевкин, 2008
Предыдущие статьи:
- Координатная плоскость
- Координатная прямая
- Уравнение с одной переменной
- Математика, 4 класс, методическое пособие, Чекин А.Л., 2007
