Координатная плоскость.
Возьмем две координатные прямые на плоскости. Пусть одна будет x, другая – y. И пусть эти прямые будут взаимно перпендикулярны (то есть пересекаются под прямым углом). Причем точка их пересечения будет началом координат для обеих прямых, а единичный отрезок одинаков (рис. 1).
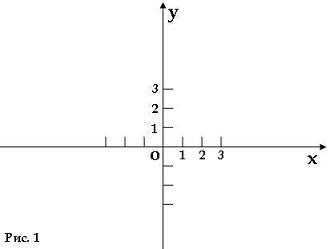
Таким образом, мы получили прямоугольную систему координат, а наша плоскость стала координатной. Прямые x и y называют осями координат. Причем, ось x – осью абсцисс, а ось y – осью ординат. Обозначается подобная плоскость обычно по названию осей и точке отсчета – xOy. Прямоугольную систему координат также называют декартовой системой координат, так как впервые ее начал активно использовать французский математик и философ - Рене Декарт.
Прямоугольные углы, образованные прямыми x и y, называют координатными углами. Каждый угол имеет свой номер как показано на рис. 2.
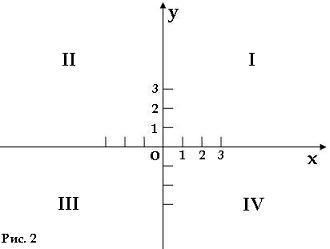
Итак, когда мы говорили про координатную прямую у всякой точки этой прямой была одна координата. Теперь, когда идет речь о координатной плоскости, то у каждой точки этой плоскости уже будут две координаты. Одна соответствует прямой x (эту координату называют абсциссой), другая соответствует прямой y (эту координату называют ординатой). Записывается это таким образом: M(x;y), где x – абсцисса, а y – ордината. Читается как: «Точка M с координатами x, y».
Как определить координаты точки на плоскости?
Теперь мы знаем, что у каждой точки на плоскости есть две координаты. Для того чтобы узнать ее координаты нам достаточно через эту точку провести две прямые, перпендикулярные осям координат. Точки пересечения этих прямых с координатными осями и будут искомыми координатами. Так, например, на рис. 3 мы определили, что координатами точки M являются 5 и 3.
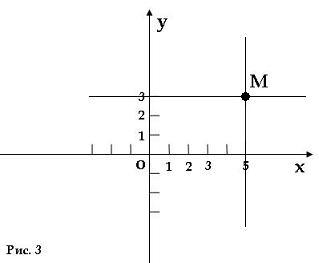
Как построить точку на плоскости по ее координатам?
Бывает и так, что мы уже знаем координаты точки на плоскости. И нам нужно найти ее расположение. Допустим у нас координаты точки (-2;5). То есть, абцисса равна -2, а ордината равна 5. Возьмем на прямой x (оси абсцисс) точку с координатой -2 и проведем через нее прямую a, параллельную оси y. Заметим, что любая точка на этой прямой будет иметь абсциссу равную -2. Теперь найдем на прямой y (оси ординат) точку с координатой 5 и проведем через нее прямую b, параллельную оси x. Заметим, что любая точка на этой прямой будет иметь ординату равную 5. На пересечении прямых a и b как раз и будет находиться точка с координатами (-2;5). Обозначим ее буквой P (рис. 4).
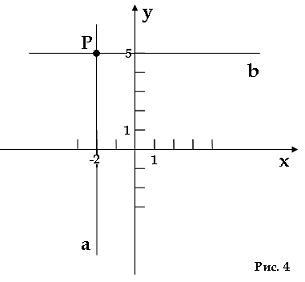
Добавим также, что прямая a, все точки которой имеют абсциссу -2, задается уравнением
x = -2 или что x = -2 – уравнение прямой a. Можно для удобства говорить не «прямая, которая задается уравнением x = -2», а просто «прямая x = -2». Действительно, для любой точки прямой a справедливо равенство x = -2. А прямая b, все точки которой имеют ординату 5, в свою очередь задается уравнением y = 5 или что y = 5 – уравнение прямой b.
Дата публикации:
Теги: алгебра :: 7 класс :: геометрия :: координатная плоскость
Смотрите также учебники, книги и учебные материалы:
Следующие учебники и книги:
- Методика обучения математике в начальной школе, Зайцева С.А., Румянцева И.Б., Целищева И.И., 2008
- Алгебра и начала математического анализа, книга для учителя, 11 класс, базовый и профил, уровни, Потапов М.К., Шевкин А.В., 2009
- Алгебра и начала математического анализа, книга для учителя, 10 класс, Потапов, Шевкин, 2008
- Линейное уравнение первой степени с двумя переменными
Предыдущие статьи:
- Координатная прямая
- Уравнение с одной переменной
- Математика, 4 класс, методическое пособие, Чекин А.Л., 2007
- Математика, 3 класс, методическое пособие, Чекин А.Л., 2006
